Question

Answer please i dont wanna fail this test

Answer 1

Answer is C.

Step-by-step explanation:

So we have 100 data, aka numbers. So the mean would be

`(x_1 + x_2 + x_3 + \cdots + x_(100))/(100) = 267`

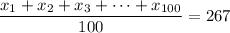
where bunch of x represents those data.

So then
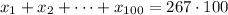
`x_1 + x_2 + \cdots + x_(100) = 267\cdot100`, right?

So we have six outliers with mean 688. That would be

`\frac{x_(i_1) + x_(i_2) + \cdots + x_(i_6)}6 = 688`

So then
`x_(i_1) + x_(i_2) + \cdots + x_(i_6) = 688\cdot6`

Now we don't know what i₁, i₂, etc, but we can just subtract outliers from set of observations and we will know that outliers will be gone in set of observation.

So that would be

`(x_1 + \cdots + x_(100))- (x_(i_1) + \cdots + x_(i_6)) = 267\cdot100 - 688\cdot6`

Now we know that there are now 94 remaining observations. So to find mean, we just divide whole thing by 94.


`((x_1 + \cdots + x_(100))- (x_(i_1) + \cdots + x_(i_6)))/(94) = (267\cdot100 - 688\cdot6)/(94) = \boxed{240.12766}`

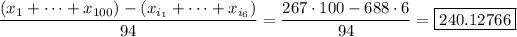
Which matches C.

Hope this helps.