Question

Find the zeros and the multiplicity of:
f(x) = x²(2x + 3)5(x − 4)²

Answer 1

`\textsf{$x=0$ with multiplicity 2.}`

`\textsf{$x=-(3)/(2)$ with multiplicity 5.}`

`\textsf{$x=4$ with multiplicity 2.}`

Explanation:

The multiplicity of a zero refers to the number of times the associated factor appears in the factored form of the equation of a polynomial.

Given polynomial:

`f(x)=x^2(2x+3)^5(x-4)^2`

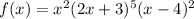
To find the zeros of the given polynomial in factored form, set each factor to zero and solve for x:

`\implies x^2=0 \implies x=0`

`\implies 2x+3=0 \implies x=-(3)/(2)`

`\implies x-4=0 \implies x=4`

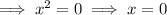
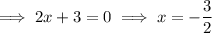
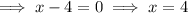
As the factor "x" appears twice in the factored form of the polynomial, the associated zero has multiplicity 2.

As the factor (2x - 3) appears five times in the factored form of the polynomial, the associated zero has multiplicity 5.

As the factor (x - 4) appears twice in the factored form of the polynomial, the associated zero has multiplicity 2.

Solution

`\textsf{$x=0$ with multiplicity 2.}`

`\textsf{$x=-(3)/(2)$ with multiplicity 5.}`

`\textsf{$x=4$ with multiplicity 2.}`

Answer 2

Given function:

• f(x) = x²(2x + 3)⁵(x - 4)²

Zero's are:

1.

• x² = 0
• x = 0, multiplicity of 2

2.

• (2x + 3)⁵ = 0
• 2x + 3 = 0
• x = - 1.5, multiplicity of 5

3.

• (x - 4)² = 0
• x - 4 = 0
• x = 4, multiplicity of 2