Question

If P(not yellow) = 4/15, which best describes the probability of the complement of the event?

A. P(yellow) = 8/15
B. P(yellow) = 11/15
C. P(not yellow) = 8/15
D. P(not yellow) = 11/15

Answer 1

Answer: The correct option is (B)
`\textup{P(yellow)}=(11)/(15).`

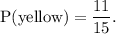
Step-by-step explanation: Given that the probability of an event of not yellow is as follows:

`\textup{P(not yellow)}=(4)/(15).`

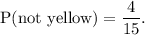
We are given to find the probability of the complement of the event.

The probability of the complement of an event A

is given by

`\textup{P(A}^\prime)=1-\textup{P(A)}.`

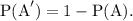
The complement of an event of NOT YELLOW will be YELLOW.

Therefore, the probability of the complement of the event is

`\textup{P(yellow)}=1-\textup{P(not yellow)}=1-(4)/(15)=(11)/(15).`

Thus, the required probability is

`\textup{P(yellow)}=(11)/(15).`

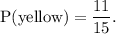
Option (B) is correct.

Answer 2

Answer: B. P(yellow) = 11/15

Step-by-step explanation: A:event that it is not yellow

B(complement of A):event that it is yellow

P(B)=1-P(A)

⇒ P(B)=1-
`(4)/(15)`

⇒ P(B)=
`(15-4)/(15)`

⇒ P(B)=
`(11)/(15)`

⇒ P(yellow)= 11/15