Answer: The correct option is (A) (3, -3).
Step-by-step explanation: We are given to solve the following system of equations :

We will be using the method of ELIMINATION to solve the given system.
Multiplying equation (i) by 3 and equation (ii) by 2, we have

and

Adding equations (iii) and (iv), we get
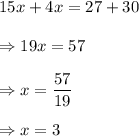
And from equation (i), we get
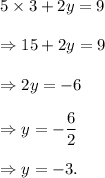
Thus, the required solution is (x, y) = (3, -3).
Option (A) is CORRECT.