Question

Divide (-5w^10+10w^8+5w^6)/(5w^5)

Answer 1

The easiest way to do this is to split that numerator up into each of its individual expressions over the denominator, like this:
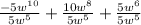
`(-5w^(10))/(5w^5)+ (10w^8)/(5w^5)+ (5w^6)/(5w^5)` and then divide each expression one at a time. In the first expression, -5 diivided by 5 = -1. Now for the exponents. As long as the base is the same you will subtract the exponents, lower from upper. Our bases are all w's, so we're good.
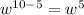
`w^(10-5)=w^5` so that expression is
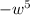
`-w^5`. Now for the second expression. 10 divided by 5 is 2, and, using our rules for dividing exponents with like bases,
`w^(8-5)=w^3`. So that expression is
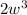
`2w^3`. For the last term there, 5 divided by 5 is 1, and
`w^(6-5)=w^1=w`. Now we will put all of them together to get a final solution of
`-w^5+2w^3+w`. There you go!