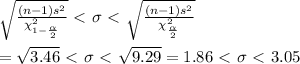Given that the standard deviation, s = 2.3 and that there are 24 students, thus the degree of freedom is 24 - 1 = 23.
For 90% confidence interval,

and
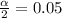
From the chi-square table, the value of
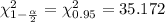
and the value of
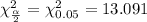
.
The 90% confidence interval for
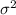
is given by:

And the 90% confidence interval for
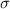
is given by: