Question

Which of the following expressions is a fourth root of unity?

a.) -1
b.) i
c.) -i
d.) all of the above

Answer 1

The CORRECT answer is D. All of the above

Explanation:

I just took the test and got it correct!

(see screen shot for proof)

Answer 2

We have to evaluate the fourth roots of unity.

For each natural number say 'n', there are exactly 'n' nth roots of unity which is expressed in the form as

`z=e^{(i2\Pi k)/(n)}`

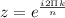
where k=0,1,2,.... n-1

Since we have to evaluate the fourth root of unity.

Therefore, we take k=0,1,2,3 and n=4

So, we get
`z=e^{(i2\Pi k )/(4)}`

`z=e^{(i\Pi k )/(2)}`

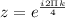
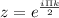
Now, For k=0, we get our first root as:

`z=e^{(i\Pi * 0 )/(2)}`

`z=e^(0) = 1`

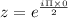
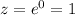
First root = 1

Now, for k=1, we get

`z=e^{(i\Pi * 1 )/(2)}`

`z=e^{(i\Pi )/(2)}`

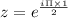
`e^(i\Theta )= \cos \Theta +i\sin \Theta` (Eulers Formula)

So,
`e^{i(\Pi )/(2)}=\cos (\Pi )/(2)+i\sin (\Pi )/(2)`

`= 0 +i = i`

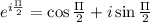
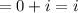
So, second root = i

Now, for k=2, we get

`z=e^{(i\Pi * 2)/(2)}`

`z=e^(i\Pi )`

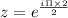
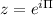
`e^(i\Theta )= \cos \Theta +i\sin \Theta` (Eulers Formula)

So,
`e^(i\Pi )=\cos \Pi +i\sin \Pi`

`= -1 +0 = -1`

Third root = -1

Now, for k=3, we get

`z=e^{i(3\Pi )/(2)}`

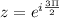
`e^(i\Theta )= \cos \Theta +i\sin \Theta` (Eulers Formula)

So,
`e^{i(3\Pi )/(2)}=\cos (3\Pi )/(2)+i\sin (3\Pi )/(2)`

`= 0 -i = -i`

So, fourth root = -i

Hence, all the fourth roots of unity are 1, i, -1 and -i

Therefore, option D is correct as all the given roots in option A, B and C are the fourth roots of unity.