Answer:
option: B (
) is correct.
Explanation:
We are given the solution set as seen from the graph as:
(-4,2)
1)
On solving the first inequality we have:
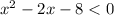
On using the method of splitting the middle term we have:
⇒
⇒
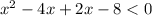
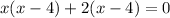
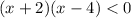
And we know that the product of two quantities are negative if either one of them is negative so we have two cases:
case 1:
and
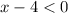
i.e. x>-2 and x<4
so we have the region as:
(-2,4)
Case 2:
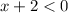and
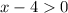
i.e. x<-2 and x>4
Hence, we did not get a common region.
Hence from both the cases we did not get the required region.
Hence, option 1 is incorrect.
2)
We are given the second inequality as:
On using the method of splitting the middle term we have:
⇒
⇒
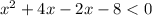
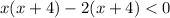
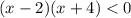
And we know that the product of two quantities are negative if either one of them is negative so we have two cases:
case 1:
and
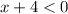
i.e. x>2 and x<-4
Hence, we do not get a common region.
Case 2:
and
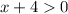
i.e. x<2 and x>-4
Hence the common region is (-4,2) which is same as the given option.
Hence, option B is correct.
3)
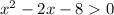
On using the method of splitting the middle term we have:
⇒
⇒
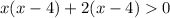
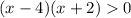
And we know that the product of two quantities are positive if either both of them are negative or both of them are positive so we have two cases:
Case 1:
and
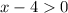
i.e. x>-2 and x>4
Hence, the common region is (4,∞)
Case 2:
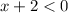and
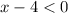
i.e. x<-2 and x<4
Hence, the common region is: (-∞,-2)
Hence, from both the cases we did not get the desired answer.
Hence, option C is incorrect.
4)
On using the method of splitting the middle term we have:
⇒
⇒
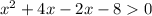
And we know that the product of two quantities are positive if either both of them are negative or both of them are positive so we have two cases:
Case 1:
and
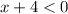
i.e. x<2 and x<-4
Hence, the common region is: (-∞,-4)
Case 2:
and
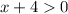
i.e. x>2 and x>-4.
Hence, the common region is: (2,∞)
Hence from both the case we do not have the desired region.
Hence, option D is incorrect.