Question

11) A fireman is standing 30 m directly west of a burning building. His ladder reaches 50 m up the side of the building. What is the angle of elevation (to the closest degree) of his ladder? A) 48°

Answer 1

tan of the angle = opposite side / adjacent = 50/30 = 1 .667

the angles measure is 59 degrees

Answer 2

The angle of elevation of his ladder is
`59^(\circ)`.

Explanation:

Given : A fireman is standing 30 m directly west of a burning building. His ladder reaches 50 m up the side of the building.

To find : What is the angle of elevation (to the closest degree) of his ladder?

Solution :

Let us assume that ladder is making a right triangle with the burning building

Let
`\theta` be the angle of elevation of his ladder.

Then apply trigonometry,

`\tan\theta = \frac{\text{Perpendicular}}{\text{Base}}`

`\Rightarrow \tan\theta=\frac{\text{height of building reached by ladder}}{\text{distance between ladder and building}}`

`\Rightarrow\tan\theta=(50)/(30)=1.67\\\\\Rightarrow\theta=\tan^(-1)(1.67)\\\\\Rightarrow\ x=59.03^(\circ)\approx59^(\circ)`

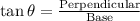
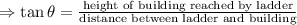
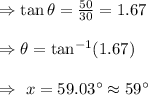
Therefore, The angle of elevation of his ladder is
`59^(\circ)`.

Refer the attached figure below.