Question

The two-way table shows the results of a recent study on the effectiveness of the flu vaccine.

What is the probability that a randomly selected person who tested positive for the flu is vaccinated?

Answer 1

The probability that a randomly selected person who is tested positive is vaccinated is:

0.4895

Explanation:

We are given a two-way frequency table that represents the result of a recent study on the effectiveness of the flu vaccine.

The table is as follows:

Pos. Neg. Total

Vaccinated 465 771 1236

Not vaccinated 485 600 1085

Total 950 1371 2321

Now we are asked to find the probability that a randomly selected person who tested positive for the flu is vaccinated.

Let A denote the event that the person is tested positive.

Let B denote the vent that he/she is vaccinated.

A∩B denote the event that the person tested positive is vaccinated.

Let P denote the probability of an event.

We are asked to find:

P(B|A)

We know that:

`P(B|A)=(P(A\bigcap B))/(P(A))`

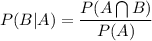
From the table we have:

`P(A\bigcap B)=(465)/(2321)`

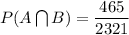
and

`P(A)=(950)/(2321)`

Hence,

`P(B|A)=((465)/(2321))/((950)/(2321))\\\\P(B|A)=(465)/(950)\\\\P(B|A)=0.4895`

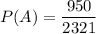
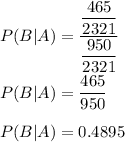
Hence, the probability is:

0.4895

Answer 2

49 %

465 + 485 = 950

465/950 = .489

.489 * 100 = 48.9, round up for 49 to get 49%, since it's only focused on people who tested positive, you would only have to compare the people in that column