Question

The circle below is centered at the origin and has a radius of 5. What is its equation?

Answer 1

`\bf \textit{equation of a circle}\\\\ (x- h)^2+(y- k)^2= r^2 \qquad center~~(\stackrel{0}{ h},\stackrel{0}{ k})\qquad \qquad radius=\stackrel{5}{ r} \\\\\\ (x-0)^2+(y-0)^2=5^2\implies x^2+y^2=25`

Answer 2

Answer: The correct option is

(B)
`x^2+y^2=25.`

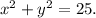
Step-by-step explanation: Given that the circle shown in the graph is centered at the origin and has a radius of 5 units.

We are to find the equation of the circle.

The STANDARD equation of a circle with center at the point (h, k) and radius of length r units is given by

`(x-h)^2+(y-k)^2=r^2~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

According to the given condition, we have

center, (h, k) = (0, 0) and radius, r = 5 units.

So, from equation (i), we get

`(x-0)^2+(y-0)^2=5^2\\\\\Rightarrow x^2+y^2=25.`

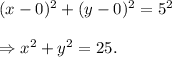
Thus, the required equation of the circle is
`x^2+y^2=25.`

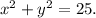
Option (B) is CORRECT.