Answer:
305 feet
Explanation:
Refer the attached figure :
The angle of elevation from Madison to the top of the Statue of Liberty is 79 degrees i.e.∠ABE=79°
Madison is standing 58.2 feet from its base i.e.BE=CD=58.2 feet
She is 5 feet tall i.e. BC=ED=5 feet.
We are supposed to find the height of the Statue of Liberty i.e. AD
In ΔABE
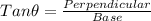
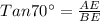
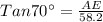

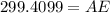
AD = AE+ED = 299.4099+5 =304.409
Hence the height of the Statue of Liberty is 304.40 feet≈ 305 feet.