Answer:
 , assuming that the object was initially not moving.
, assuming that the object was initially not moving.
Step-by-step explanation:
Under the assumptions, the acceleration
 of this object will be constant:
of this object will be constant:
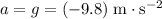 .
.
The initial velocity
 of this object will be
of this object will be
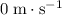 since this object was initially not moving:
since this object was initially not moving:
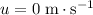 .
.
Let
 denote the displacement of this object. This object has been accelerating for
denote the displacement of this object. This object has been accelerating for
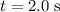 . Apply the SUVAT equation
. Apply the SUVAT equation
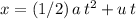 to find the displacement of this object in that much time:
to find the displacement of this object in that much time:
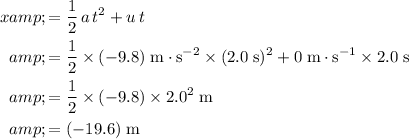 .
.
In other words, the displacement of this object would be
 (displacement is negative since this object is now below where it initially was.)
(displacement is negative since this object is now below where it initially was.)