Question

Which of the following represents a recursive sequence?

A.
a(n)=3(n)-2
B.
a(n)=3x3^(n-1)
C.
a(n)=3xa(n-1)
D.
a(n)=3

Answer 1

Option C is correct.

`a_n=3 a_(n-1)`

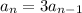
Explanation:

For a sequence
`a_1, a_2, a_3, . . . , a_n, . . .`

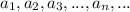
A recursive formula is a formula that requires the computation of all previous terms in order to find the value of
`a_n`

There is two simple examples of recursive definitions are for:

Arithmetic sequences and geometric sequences.

An arithmetic sequence has a common difference(d) or a constant difference between each term.

Then the recursive formula for arithmetic sequence is:

`a_n = a_(n-1)+d`

Next,

for geometric sequence has a common ratio(r)

the recursive formula is given by;

`a_n = ra_(n-1)`

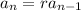
Therefore, from the given options you can see that the only option C which represents the recursive sequence is,
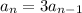`a_n=3 a_(n-1)` where r =3 is the common ratio.