Answer:
q#1 Option B.2 possible solution is correct option
Q#2 option c. 1 viable solution is correct option.
Explanation:
Q#1
y=4
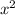 +3x+45
+3x+45
as this is a quadratic solution
and we know that when we solve a quadratic equation then it gives two possible solutions
hence option b is the correct option
Q#2
option c is correct option when we solve an quadratic equation it gives two solution one is positive and other is negative as we know that income cannot be negative
hence only one viable solution exists when we solve this
y=4
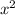 +3x+45 quadratic equation
+3x+45 quadratic equation