Question

If a square plate has side lengths of 5 inches, what is the length of the diagonal to the nearest tenth of an inch?

Answer 1

Use the Pythagoras theorem:-

diagonal^2 = 5^2+5^2 = 50
diagonal = sqrt 50 = 7.1 inches to nearest tenth

Answer 2

It is given that the plate is a square.

Therefore, let us represent the side of the square by the variable, "a".

Therefore, it is given to us that:
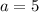`a=5` inches.

Now, we have to find the diagonal of the square. We know that the diagonal,
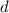`d` of a square is given by the formula:

`d=a√(2)`

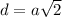
Applying the above formula to our case we get the diagonal to be as:

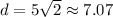`d=5√(2)\approx7.07` inches.

Therefore, the length of the diagonal to the nearest tenth of an inch is:

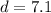`d=7.1` inches.