Question

Amelia, Luis, Shauna, and Clarence used different approaches to solve the inequality 7.2b + 6.5 > 4.8b – 8.1. Amelia started by subtracting 7.2b from both sides to get 6.5 > –2.4b – 8.1. Luis started by subtracting 4.8b from both sides to get 2.4b + 6.5 < – 8.1. Shauna started by subtracting 6.5 from both sides to get 7.2b > 4.8b – 14.6. Clarence started by adding 8.1 to both sides to get 7.2b + 14.6 > 4.8b. Which student’s first step was incorrect, and why? Amelia’s, because the variable term must be isolated on the left side Luis’s, because he flipped the inequality sign when he subtracted Shauna’s, because she did not apply the subtraction property of equality properly Clarence’s, because the terms he added together were not like terms

Answer 1

the answer would be B 

Answer 2

Luis’s, because he flipped the inequality sign when he subtracted

Explanation:

Here, the given inequality,

`7.2b + 6.5 > 4.8b - 8.1`

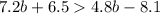
Since, Amelia started by subtracting 7.2b from both sides to get 6.5 > –2.4b – 8.1,

By the subtraction property of inequality,

The answer will not change,

Thus, her first step is not incorrect.

Luis started by subtracting 4.8b from both sides to get 2.4b + 6.5 < - 8.1,

He flipped the sign of inequality when he applied subtraction property of inequality which is wrong,

⇒ His first step is incorrect.

Shauna started by subtracting 6.5 from both sides to get 7.2b > 4.8b – 14.6.

By the subtraction property of inequality,

The answer will not change,

Thus, her first step is not incorrect.

Clarence started by adding 8.1 to both sides to get 7.2b + 14.6 > 4.8b,

By the Additive property of inequality,

The answer will not change,

Thus, his first step is not incorrect.

Hence, only Luis's first step was incorrect.