Question

Find the indicated limit, if it exists.

Answer 1

Ans: 7 ( limit does exist)

Step-by-step explanation:
The limit exists only if we apply the limits -be it left hand or right hand- the answers to both should be 7 because at x = 0 the value is constant.

Left hand limit( x < 0):

`\lim_(x \to 0) 7-x^2 = 7-(0)^2 = 7`

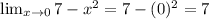
Right hand limit (x > 0):

`\lim_(x \to 0) -10x + 7 = -10(0) + 7 = 7`

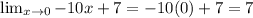
Since upon applying the limits, the answers to all is 7 (same). Hence limit exists!