Question

A college is creating a new rectangular parking lot. the length is 0.17 mile longer than the width and the area of the parking lot is 0.039 square mile. find the length and width of the parking lot.

Answer 1

Let
x----------> the length of the parking lot
y----------> the width of the parking lot

we know that
x=0.17+y-------->equation 1
0.039 mi²=x*y---------> equation 2

substitute 1 in 2
0.039=[0.17+y]*y----------> 0.039=0.17y+y²-----> y²+0.17y-0.039=0

using a graph tool-----> to resolve the second order equation
see the attached figure

the solution is
y=0.13 mi
x=0.17+y------> x=0.17+0.13------> x=0.30 mi

the answer is
the length of the parking lot is 0.30 miles
the width of the parking lot is 0.13 miles

Answer 2

Let's call the width of the parking lot w.
The length of the parking lot if .17 more than the width so the length is w + .17

The parking lot is rectangular so its area is found by multiplying the length and the width. That is, the area is equal to what we obtain when we multiply w by w+.17. The area is:
`A = w(w+.17)= w^(2) +.17w`

We are also told that the area is equal to .039 square miles so we set the expression we obtained for the area equal to .039 as follows.


`w^(2) +.17w=.039`

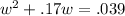
Since w represents the width of the rectangular lot, we can solve this equation for w to find the width. This is a quadratic equation (the highest exponent of the variable w is 2). We solve these by setting them equal to zero and then using the quadratic formula.

Setting our equation equal to zero (subtract .039 from both sides) gives us:

`w^(2) +.17w-.039=0`

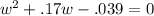
The quadratic formula is as follows. Since the equation is in terms of w we write it as "w = ..." instead of the usual "x = ..."


`w= \frac{-bplusminus \sqrt{ b^(2) -4ac} }{2a}`

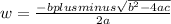
The part I write as "plusminus" is typically written with a + sign over a - sign. For right now let's leave it at that. Later in the problem we will see what it means and what to do with it.

To use the formula we have to identify a, b and c.

a is the coefficient of the squared term. That is, the number in front of
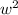
`w^(2)` which here is 1.

b is the coefficient of the linear term. That is, the number in front of w which here is .17

c is the constant (the number by itself0 which is -.039

So we have:
a=1
b=.17
c=-.039

We plug these into the quadratic formula to obtain:

`w= \frac{-.17plusminus \sqrt{ .17^(2) -(4)(1)(-.039)} }{(2)(1)}`

`w= (-.17plusminus √( .0289+.156) )/(2)`

`w= (-.17plusminus √( .189) )/(2)`

`w= \frac{-.17plusminus.43} {2}`

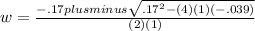
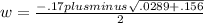
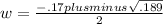
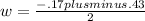
Here is where the "pluminus" comes in. We continue to simplify the expression on the right but we split it in two. In one case we use "plus" and in the other "minus". That is, we add in one and subtract in the other. This gives us:

`w= (-.17+.43)/(2)= (.26)/(2)=.13`
and

`w= (-.17-.43)/(2)= (-.6)/(2)=-.3`

w is the width of the rectangular lot so it is a distance and cannot be measured using negative numbers. The width of the rectangular must be positive so we disregard the negative answer.

The width of the rectangle is .13 miles

Recall that the length of the rectangle is .17 more than the width. That is, the length is w+.17 and as we know the width to be .13 miles the length is .13 + .17 = .3 miles

The answer therefore is:
width = .13 miles
length = .3