Answer: The correct option is (2)
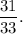
Step-by-step explanation: Given that the numerator and the denominator of a fraction are consecutive odd numbers.
Also, if nine is subtracted from the numerator, the ratio of the numerator to the denominator of the new fraction is two to three.
we are to find the fraction.
Let
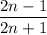 be the given fraction, where n is an integer.
be the given fraction, where n is an integer.
Then, according to the given information, we have
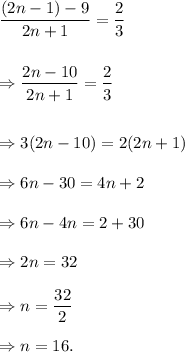
Therefore, the required fraction will be
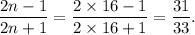
Thus, the fraction is
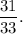
Option (2) is CORRECT.