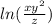Question

What is lnx+2lny−lnz written as a single logarithm?

Answer 1

`\ln x+2\ln y-\ln z=\ln x+\ln y^2-\ln z=\ln(xy^2)/(z)\\\\Used:\ln a+\ln b=\ln(a\cdot b}\\\\\ln a-\ln b=\ln(a)/(b)\\\\n\ln a=\ln a^n`

Answer 2

`ln((xy^(2))/(z))`

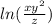
Explanation:

3 rules of logarithms that we are going to use on this is:

1. 
   `ln(a+b)=ln(a*b)`
2. 
   `ln(a-b)=ln((a)/(b))`
3. 
   `bln(a)=ln(a)^(b)`

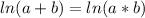
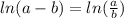
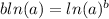
We can use the third rule to simplify the expression as:

`ln(x)+2ln(y)-ln(z)\\=ln(x)+ln(y^(2))-ln(z)`

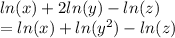
Simplifying the first 2 terms using first rule gives us:

`ln(x*y^(2))-ln(z)`

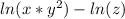
Now using the second rule to further simplify and write as single logarithm gives us:

`ln((xy^(2))/(z))`