Answer:The smallest angle of the triangle will be nearest to 41°.
Step-by-step explanation:
since, the sides of the triangle are 4,5 and 6.
when we talk about the smallest angle then it must be the opposite angle of side 4.
Thus according to the law of cosines,
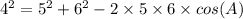 (where A(let) be the smallest angle of the triangle.)
(where A(let) be the smallest angle of the triangle.)
⇒16=25+36-60cos(A)
⇒16-61=-60cos(A)
⇒-45=-60cos(A)
⇒
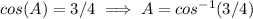 ⇒A=41.4096221093 degree
⇒A=41.4096221093 degree
 41°
41°