Consider this option:
1. ∠AYC+∠CYD+∠DYB=180°; ⇒
5z+90°+z=180°; ⇒
z=15°; ⇒
∠AYC=5z=75°; ∠DYB=15°.
2. Note, that ∠CAF=∠BAE, then
∠BAE+∠CAF+∠CAH+∠HAG+GAE=360-160; ⇒ 2∠CAF+5x=110° (The first equation of the system).
∠GAE+∠HAG+∠CAH+∠CAF=180°;⇒ 5x+∠CAF=90° (The second equation of the system).
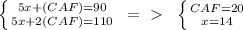
It means, that x=∠CAH=14°; 4x=∠EAG=56°