Answer:
The approximate measure of angle ACB is 53.13°
Explanation:
Given,
In the right triangle ABC,
AC = 25 cm,
BC = 15 cm,
Where, AC is the hypotenuse of the triangle,
⇒ ∠B = 90°
By the pythagoras theorem,
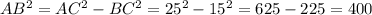

Now, by the law of sine,
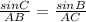

By substituting the values,
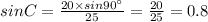
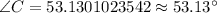
Hence, the approximate measure of angle ACB is 53.13°