Answer:
Sin θ =
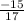 and
and
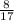 .
.
Explanation:
Given : cot θ = -8/15.
To find : sin θ and cos θ.
Solution : We have given
cot θ =
 .
.
cot θ =
 .
.
 =
=
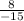 .
.
Hypotenuse =

Hypotenuse =
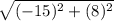 .
.
Hypotenuse =
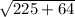 .
.
Hypotenuse =
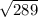 .
.
Hypotenuse =17 .
Sin θ =
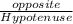 .
.
Plugging the values.
Sin θ =
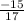 .
.
Cos θ =
 .
.
Cos θ =
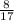 .
.
Therefore, Sin θ =
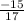 and
and
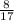 .
.