Question

If a town with a population of 10,000 doubles every 14 years, what will the population be in 42 years and is it modeled by a linear function or an exponential function?

Answer 1

80,000 will be the population in 42 years. It is an exponential function.

Explanation:

If a town with a population of 10,000 doubles every 14 years.

Initial population of a town is 10,000

Point: (0,10000)

It's double every 14 years.

Point: (14,20000)

Let us suppose exponential function
`y=ab^x`

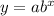
Now using both point to find a and b

`10000=a\cdot b^0\Rightarrow a=10000`

Using point (14,20000) and a=10000 to solve for b

`20000=10000\cdot b^(14)`

`2=b^(14)`

`b=2^(1/14)`

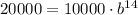
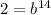
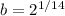
Exponential function:

`y=10000(2)^{(x)/(14)}`

We need to find y at x=42

So, we put x=42 into function and solve for y

`y=10000(2)^{(42)/(14)}`

`y=10000(2)^3`

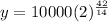
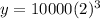
y=80,000

Thus, 80,000 will be the population in 42 years. It is an exponential function.