2 Answers

Kabindas · Answer 1 · 2019-10-18T06:07:21+0000

Answer:

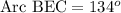
$\text{Arc BEC}=134^o$

Explanation:

We have been given an image of a circle and we are asked to find the measure of arc BEC.

We can see that angle ABC is inscribed angle and measure of an inscribed angle is one half the measure of its subtended arc.

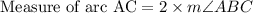
$\text{Measure of arc AC}=2* m\angle ABC$

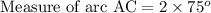
$\text{Measure of arc AC}=2* 75^o$

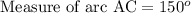
$\text{Measure of arc AC}=150^o$

Since we know that the circumference of a 360 degree, so we can set an equation to find the measure of arc BEC as:

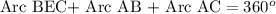
$\text{Arc BEC+ Arc AB + Arc AC}=360^o$

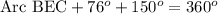
$\text{Arc BEC}+76^o+150^o=360^o$

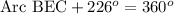
$\text{Arc BEC}+226^o=360^o$

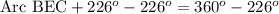
$\text{Arc BEC}+226^o-226^o=360^o-226^o$

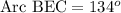
$\text{Arc BEC}=134^o$

Therefore, the measure of arc BEC is 134 degrees.

Please log in or register to add a comment.