Question

Which of the following statements are true about the equation below?

x^2-6x+2=0

( 1 ) The graph of the quadratic equation has a minimum value.
( 2 ) The extreme value is at the point (3,-7).
( 3 ) The extreme value is at the point (7,-3).
( 4 ) The solutions are x = -3 + or - the square root of 7 .
( 5 ) The solutions arex = 3 + or - the square root of 7.
( 6 ) The graph of the quadratic equation has a maximum value.

Answer 1

Option 1, 2, 5 are the correct answer.

Step-by-step explanation:

We have the quadratic equation,
`x^2-6x+2=0`

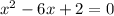
First derivative of the equation is given by 2x - 6 = 0

So x = 3

At x = 3 the value of quadratic equation is extreme, corresponding y is given by
`3^2-6*3+2=11-18=-7`, So extreme value is at (3,-7)

Second derivative of the quadratic equation is given by 2 ( positive value)

Second derivative is positive so graph of equation has a minimum value.

Now root of the equation
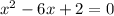`x^2-6x+2=0` is given by

`\frac{6+√((-6)^2-4*1*2)} {2} =3+√(7)`

or

`\frac{6-√((-6)^2-4*1*2)} {2} =3-√(7)`

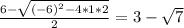
Option 1, 2, 5 are the correct answer.