The compounded interest function that models the situation is:
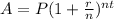
where
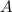
is the final amount of money after
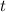
years.
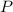
is the initial investment.

is the interest rate in decimal form.

is the number of times the interest is compounded per year.
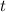
is the time in years.
We know for our problem that
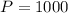
and
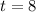
. To convert the interest rate to decimal form, we are going to divide the rate by 100%:
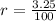
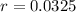
We also know that the interest is compounded anally, so it is compounded 1 time per year; therefore,
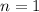
.
Lets replace the values in our formula to find the final amount after 8 years:
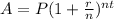
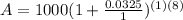
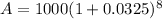
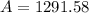
We can conclude that since we are dealing with compound interest we must use the function
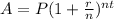
. Also, after 8 years the balance in the account will be $1291.58