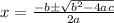Question

Complete the steps of the derivation of the quadratic formula. Step 2: Step 3: Step 4: Step 5:

Answer 1

Step 1
(x+b/2a)^2-[(b²-4ac)/4a^2]=0
Step 2
(x+b/2a)^2=(b²-4ac)/4a^2
Step 3
getting the square root of both sides we get
x+b/2a=√(b²-4ac)/4a^2
x+b/2a=+/-√(b²-4ac)/2a
Step 4
subtract b/2a from both sides we get:
x+b/2a-b/2a=-b/2a+/-√(b²-4ac)/2a
x=-b/2a+/-√(b²-4ac)/2a
Step 5
Simplifying the above by putting them under the same denominator we get
x=[-b+/-√(b²-4ac)]/2a

Answer 2

To complete the derivation of the quadratic equation:

Given:

`(x+(b)/(2a))^2-(b^2-4ac)/(4a^2) = 0`

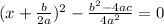
Add both sides
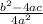`(b^2-4ac)/(4a^2)` we have;

`(x+(b)/(2a))^2=(b^2-4ac)/(4a^2)`

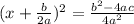
Taking square root both sides we have;

⇒
`(x+(b)/(2a))= \pm \sqrt{(b^2-4ac)/(4a^2)}`

⇒
`x+(b)/(2a) =\pm (√(b^2-4ac))/(2a)`

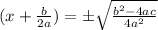
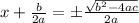
Subtract
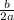`(b)/(2a)` from both sides we have;

`x =-(b)/(2a) \pm (√(b^2-4ac))/(2a)`

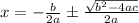
Therefore, complete derivation for the quadratic equation is:

Step 1.

`(x+(b)/(2a))^2-(b^2-4ac)/(4a^2) = 0`

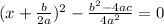
Step 2.

`(x+(b)/(2a))^2=(b^2-4ac)/(4a^2)`

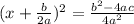
Step 3.

`(x+(b)/(2a))= \pm \sqrt{(b^2-4ac)/(4a^2)}`

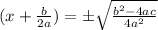
Step 4.

`x+(b)/(2a) =\pm (√(b^2-4ac))/(2a)`

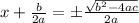
Step 5.

`x =-(b)/(2a) \pm (√(b^2-4ac))/(2a)`

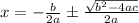
or

`x = (-b \pm √(b^2-4ac))/(2a)`