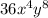Question

Please help me someone

Answer 1

To solve this, you need to know three exponent rules:
1) Power of a product
Basically says
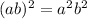
`(ab)^(2) = a^(2) b^(2)`. This means a product raised to a power is the same as taking each factor to that power and multiplying them.

For example:
`(5a)^(2) = 5^(2) a^(2)`

2) Product of powers
Basically says
`a^(m) a^(n) = a^(m+n)`. When two expressions with the same base (a) are multiplied, you can add their exponents while keeping the same base.

For example:
`a^(2) a^(3) = a^(2+3) = a^(5)`

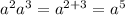3) Power of a power
Basically says
`(a^(m))^(n) = a^(m * n)`. When an exponent is being raised to a exponent, you can multiply the exponents.

For example:
`(a^(2))^(3) = a^((2 * 3)) = a^(6)`
----

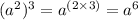
Back to your problem:
You are asked to simplify
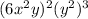
`(6x^(2) y)^(2) (y^(2))^(3)`, Tackle it by simplifying both factors and then multiplying them together and simplifying again.

1) First use the power of a product rule to change
`(6x^(2) y)^(2)` into
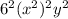
`6^(2) (x^(2))^(2) y^(2)`. Simplify it into
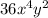
`36 x^(4) y^(2)` using the power of a power rule.

2) Simplify
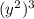
`(y^(2))^(3)` into
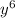
`y^(6)` using the power of a power rule.

3) Multiply the simplified factors from part one and two and simplify using the product of powers rule:

`(36 x^(4) y^(2))(y^(6))\\ = (36 x^(4))(y^(2) y^(6))\\ = (36 x^(4))(y^(2+6)) \\ = 36 x^(4)y^(8)`

---

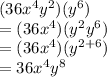
Answer:
`36 x^(4)y^(8)`