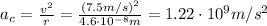Question

What is the acceleration of a proton moving with a speed of 7.5 m/s at right angles to a magnetic field of 1.7 t ?

Answer 1

The Lorentz force acting on the proton is:

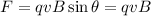
`F=qvB \sin \theta = qvB` (1)
where
q is the proton charge (
`1.6 \cdot 10^(-19) C`)
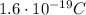
v is its speed (7.5 m/s)
B is the magnetic field intensity (1.7 T)

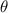
`\theta` is the angle between the direction of v and B, and since the proton is travelling at right angle to the magnetic field,
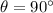
`\theta=90^(\circ)` and
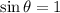
`\sin \theta = 1`, so we can ignore it.

The Lorentz force provides the centripetal force that keeps the proton in circular orbit. The centripetal force is

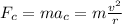
`F_c = m a_c = m (v^2)/(r)` (2)
where

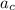
`a_c` is the centripetal acceleration
m is the proton mass (
`1.67 \cdot 10^(-27) kg)`)
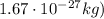
v is the proton speed

We said that the Lorentz force provides the centripetal force of the motion, so we can equalize (1) and (2) to find the radius of the proton's orbit:

`m (v^2)/(r)=qvB`

`r= (mv)/(qB)= ((1.67 \cdot 10^(-27) kg)(7.5 m/s))/((1.6 \cdot 10^(-19)C)(1.7 T))=4.6 \cdot 10^(-8) m`

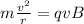
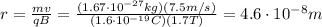
Therefore now we can calculate the centripetal acceleration of the proton, which is given by

`a_c = (v^2)/(r)= ((7.5 m/s)^2)/(4.6 \cdot 10^(-8) m)=1.22 \cdot 10^9 m/s^2`