The expression for the equation of a wave is:
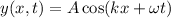
(1)
where
A is the amplitude
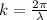
is the wave number, with
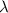
being the wavelength
x is the displacement
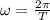
is the angular frequency, with T being the period
t is the time
The equation of the wave in our problem is
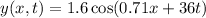
(2)
where x and y are in cm and t is in seconds.
a) Amplitude:
if we compare (1) and (2), we immediately see that the amplitude of the wave is the factor before the cosine:
A=1.6 cm
b) Wavelength:
we can find the wavelength starting from the wave number. For the wave of the problem,
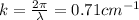
And re-arranging this relationship we find
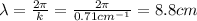
c) Period:
we can find the period by using the angular frequency:
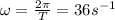
By re-arranging this relationship, we find
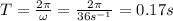
d) Speed of the wave:
The speed of a wave is given by
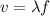
where f is the frequency of the wave, which is the reciprocal of the period:
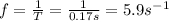
And so the speed of the wave is

e) Direction of the wave:
A wave written in the cosine form as
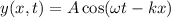
propagates in the positive x-direction, while a wave written in the form

propagates in the negative x-direction. By looking at (2), we see we are in the second case, so our wave propagates in the negative x-direction.