Question

At maximum speed, an airplane tracked 1720 miles against the wind in 5 hours. Flying with the wind, the plane can travel the same distance in 4 hours.

Let x be the maximum speed of the plane and y be the speed of the wind. What is the speed of the plane with no wind?

Answer 1

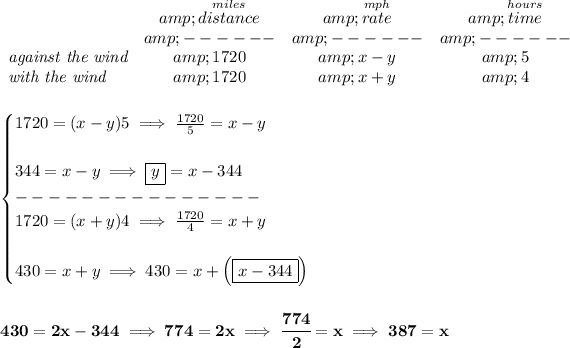
recall your d = rt, distance = rate * time.

as the plane goes against the wind, the plane is not really flying at "x" mph, but is really going slower, at " x - y ", because the wind is subtracting speed from it.

likewise, when the plane is going with the wind, is not really going at "x" mph, but at " x + y ", is going faster due to the wind, thus


`\bf \begin{array}{lccclll} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ &------&------&------\\ \textit{against the wind}&1720&x-y&5\\ \textit{with the wind}&1720&x+y&4 \end{array} \\\\\\ \begin{cases} 1720=(x-y)5\implies (1720)/(5)=x-y\\\\ 344=x-y\implies \boxed{y}=x-344\\ ---------------\\ 1720=(x+y)4\implies (1720)/(4)=x+y\\\\ 430=x+y\implies 430=x+\left( \boxed{x-344} \right) \end{cases} \\\\\\ 430=2x-344\implies 774=2x\implies \cfrac{774}{2}=x\implies 387=x`