Question

What is the measure of angle EFD?

Answer 1

`\angle EFD= 123^(\circ)`

Explanation:

We are given the following information in the question:

`\angle ECD =57^(\circ)`

FE and Fd are tangents to the given circle.

Then, by property of tangent that tangent of a circle is always perpendicular to the radius corresponding to the point where the tangent touches the circle.

Therefore,

`\angle CEF =90^(\circ)\\\angle CDF =90^(\circ)`

According to the angle sum property of quadrilateral:

`\text{In quadrilateral CEFD}\\\angle C + \angle E +\angle F + \angle D = 360^(\circ)`

Putting the values, we get,

`57 + 90 + 90+ \angle EFD = 360\\\angle EFD = 360-(57 + 90 + 90)\\\angle EFD = 123^(\circ)`

Answer 2

B.
`123^o`

Explanation:

We have been given an image of a circle and we are asked to find the measure of angle EFD.

Since we know that tangent of a circle in perpendicular to radius, so measure of angle FEC and measure of angle FDC will be 90 degrees.

Since we know that the tangent drawn from an external point of a circle are equal, so length of segment EF will be equal to the length of segment FD.

Since radii of a circle are equal, so length of CD will be equal to length of CE.

We can see that CEFD is a kite as it has two disjoint pairs of congruent sides and one pair of congruent opposite angles.

Since all the angles of a kite add up-to 360 degrees, so the measure of angle EFD will be equal to:

`m\angle EFD=360^o-(90^o+90^o+57^o)`

`m\angle EFD=360^o-(237^o)`

`m\angle EFD=123^o`

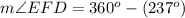
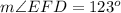
Therefore, the measure of angle EFD is 123 degrees and option B is the correct choice.