Question

Find all angles 0 theta such that 0 degrees are less than or equal to 0 theta and less than or equal to 360 degrees for which the statement sin(-104) = sin 0 theta is true

Answer 1

Hello there. To solve this question, we'll have to remember some properties about angles and the unit circle.

First, remember the unit circle:

An angle is represented as the measure between the line joining the origin and any point of the circle with the x-axis, as follows

The full angle in this case, representing a cycle in the circle is

`\theta=2\pi`

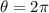
So we want to determine all angles θ between 0 and 360º such that

`\sin(-104^(\circ))=\sin(\theta)`

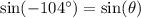
For this, we have to remember about first positive determination of an angle.

Notice we can represent negative angles in the unit circle if, instead of following in the anti-clockwise orientation (we say positive orientation), we follow the other way around:

But notice that we can represent these angles with our first case if you consider:

`2\pi-\alpha`

Since you have the property that the full angles is 2pi, hence

Thefore you have that

`360^(\circ)-104^(\circ)=256^(\circ)`

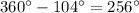
In this case notice that we added 360º to the angle, since we fixed the point of which the angle was at and gave it a full rotation.

For smaller angles, for example, -1352º, you can add the biggest possible multiple of 360º, that represents the number of full rotations you have to have in order to find its first positive determination.

In this case, we found that

`\theta=256^(\circ)`

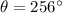
Satisfying the property that

`0\leq\theta\leq360^(\circ)`