Answer:
The possibilities of f(x) and g(x) are
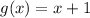 and
and

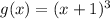 and
and

Explanation:
The given function is
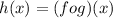 where
where
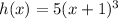
We need to find one possibility for f(x) and g(x),
One of possible solution is;
Let
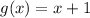
and

Another possible solution is;
Let
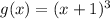
and

Therefore, the possibilities of f(x) and g(x) are
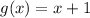 and
and

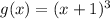 and
and
