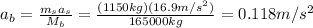For Newton's third law, for every action there is an equal and opposite reaction. This means that the force the battleship exerts on the artillery shell is equal (and opposite) to the force exerted by the shell on the battleship. Since the force is the product between the mass and the acceleration, the previous statement becomes, in formula:
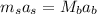
where the term on the left is the force exerted on the shell and the term on the right is the force exerted on the battleship, and where
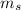
is the mass of the shell
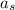
is its acceleration
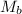
is the mass of the battleship
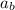
is its acceleration
By re-arranging this equation and by using the data of the problem, we can calculate
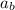
, the recoil acceleration of the battleship: