Given that the lengths of songs on the radio are normally distributed with a mean length of 210 seconds, then the probability that a randomly selected
song will have length between 194 and 226 seconds is given by:
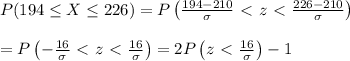
Given that the probability that all songs have lengths between 194 and 226 seconds is 38.2% = 0.382, then
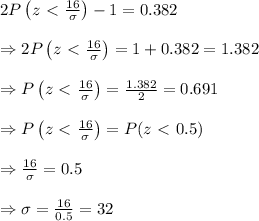
Therefore, the standard deviation of the distribution is 32 seconds.