Question

Elliott purchased a used pick-up truck for $9,500 He put $500. as a down payment and will repay the balance in monthly payments of $365. over the next 3 years. What is the APR of this loan?

Answer 1

The question will be solved using the present value of annuity formula.

Now, since he made a down payment of $500, The amount left to be paid is given $9,500 - $500 = $9,000.

The present value of annuity is given by:


`PV=P\left[ (1-\left(1+(r)/(t)\right)^(-nt))/( (r)/(t) ) \right]`

where: PV = $9,000; P = $365; t = 12 payments per year, n = 3 years; r = APR and


`\left[ (1-\left(1+(r)/(t)\right)^(-nt))/( (r)/(t) ) \right]`

is the Present value of annuity factor for
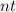
`nt` periods at
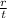
`(r)/(t)` interest rate per period.

Here, there are 3 years x 12 monthly payments = 36 periods.

Thus,


`9000=365\left[ (1-\left(1+(r)/(12)\right)^(-3*12))/( (r)/(12) ) \right] \\ \\ \Rightarrow \left[ (1-\left(1+(r)/(12)\right)^(-36))/( (r)/(12) ) \right]= (9000)/(365) =24.657534`

This means that the present value of annuity factor is 24.657534.

Using the present value of annuity table, the present value of annuity facot for 36 periods at 2% interest rate per period is 25.488842 and at 3% is 21.832253.

Let the interest rate that give the present value of annuity factor of 24.657534 be x, then interpolating, we have:


Let
`1+ (r)/(12) =x`, then we have:


`(x-2)/(3-2) = (24.657534-25.488842)/(21.832253-25.488842) = (-0.831308)/(-3.656589) =0.227345 \\ \\ \Rightarrow x-2=0.227345 \\ \\ \Rightarrow x=2+0.227345=2.227345.`

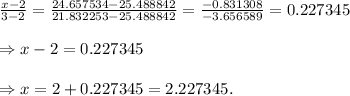
Thus, the interest rate per period (r/12) = 2.227345%.

Therefore, the APR = 12 x 2.227345 = 26.7281 ≈ 26.7%