Question

He angular position of a swinging door is described by θ = 5.00 + 10.0 t + 2.00 t2 [rad]. (a) determine the angular position, angular speed, and angular acceleration of the door at t = 3.00 s. (b) if the door starts from rest and its angular acceleration is 0.560 rad/s2, through what angle does it have to turn to reach an angular speed of 0.750 rad/s?

Answer 1

Hi there!

We are given that:

`\theta = 5 + 10t + 2t^2`

The equation for angular velocity is equivalent to the derivative of this equation, so:

`\omega(t) = (d\theta)/(dt) = 10 + 4t`

Angular acceleration is the derivative of the function for angular velocity:

`\alpha(t) = (d\omega)/(dt) = 4`

At t = 3 sec:

`\theta = 5 + 10(3) + 2(3^2) = \boxed{53 rad}`

`\omega = 10 + 4(3) = \boxed{22 rad/sec}`

`\alpha = \boxed{4 rad/sec^2}`

We can use the rotational equivalent of a kinematic equation to solve:

`\omega_f^2 = \omega_i^2 + 2\alpha\theta`

Plug in the givens:

`.750^2 = 0^2 + 2(.56)\theta\\\\(.750^2)/(2(.56)) = \theta = \boxed{0.502 rad}`

Answer 2

(a) The angular position of the door is described by

`\theta(t)=5+10t+2t^2 [rad]`

The angular velocity is given by the derivative of the angular position:

`\omega(t)=10+4t [rad/s]`

While the angular acceleration is given by the derivative of the angular velocity:

`\alpha(t)=4 [rad/s^2]`

We want to find the values of these quantities at time t=3.00 s, so we must substitute t=3.00 s into the expressions for
`\theta, \omega, \alpha`:

`\theta(3.00 s)=5+(10)(3.00 s)+2(3.00s)^2 = 53 rad`

`\omega(3.00 s)=10+4(3.00s)=22 rad/s`

`\alpha(3.00s)=4 rad/s^2`

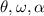
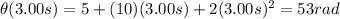
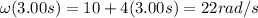
(b) The door starts from rest, so its initial angular velocity is
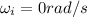
`\omega_i=0 rad/s`, and it reaches a final angular velocity of
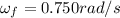
`\omega_f=0.750 rad/s` with an angular acceleration of
`\alpha=0.560 rad/s^2`. We can find the angular distance covered by the door by using the following relationship:

`2 \alpha \theta = \omega_f^2 - \omega_i^2`
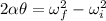
from which we find

`\theta= (\omega_f^2)/(2 \alpha)= ((0.750 rad/s)^2)/(2 \cdot 0.560 rad/s^2) =0.502 rad`