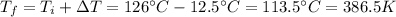Question

Five moles of an ideal monatomic gas with an initial temperature of 126 ∘c expand and, in the process, absorb an amount of heat equal to 1300 j and do an amount of work equal to 2080 j .

Answer 1

Missing question:
"What is the final temperature of the gas?"

Solution:
The first law of thermodynamics states that:

`\Delta U = Q-W`
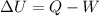
where

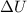
`\Delta U` is the variation of internal energy of the gas

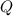
`Q` is the heat absorbed by the gas

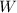
`W` is the work done by the gas

The gas in this problems absorbs
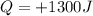
`Q=+1300 J` of heat and it does
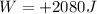
`W=+2080 J` of work, so its variation of internal energy is:

`\Delta U = 1300 J - 2080 J = -780 J`
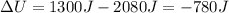
This means the gas has lost internal energy.

But the variation of internal energy is related to the variation of temperature by:

`\Delta U = (k)/(2)nR \Delta T`
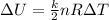
where
k is the number of degrees of freedom (k=3 for a monoatomic gas)
n is the number of moles
R is the gas constant

`\Delta T` is the variation of temperature of the gas.

Re-arranging the equation and using the variation of internal energy that we found at the previous step, we find:

`\Delta T = (2 \Delta U)/(knR)= (2 (-780 J))/(3 (5.0 mol)(8.31 J/mol K)) =-12.5 K`

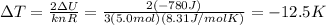
Variation of temperatures in Kelvin are equal to variation of temperatures in Celsius, so
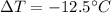
`\Delta T = -12.5 ^(\circ) C` and we can now find the final temperature of the gas:

`T_f = T_i + \Delta T=126^(\circ)C - 12.5 ^(\circ)C=113.5^(\circ)C = 386.5 K`