Question

Find the general indefinite integral. (use c for the constant of integration.) (7θ − 6 csc(θ) cot(θ)) dθ

Answer 1

`\displaystyle \int {\big[ 7\theta - 6csc(\theta)cot(\theta) \big]} \, d\theta = 6csc(\theta) + (7x^2)/(2) + C`

General Formulas and Concepts:

Calculus

Integration

• Integrals
• [Indefinite Integrals] Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

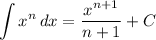
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

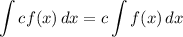
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Explanation:

Step 1: Define

Identify

`\displaystyle \int {\big[ 7\theta - 6csc(\theta)cot(\theta) \big]} \, d\theta`

Step 2: Integrate

1. [Integral] Rewrite [Integration Property - Addition/Subtraction]:
   `\displaystyle \int {\big[ 7\theta - 6csc(\theta)cot(\theta) \big]} \, d\theta = \int {7\theta} \, d\theta - \int {6csc(\theta)cot(\theta)} \, d\theta`
2. [Integrals] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {\big[ 7\theta - 6csc(\theta)cot(\theta) \big]} \, d\theta = 7\int {\theta} \, d\theta - 6\int {csc(\theta)cot(\theta)} \, d\theta`
3. [1st Integral] Reverse Power Rule:
   `\displaystyle \int {\big[ 7\theta - 6csc(\theta)cot(\theta) \big]} \, d\theta = 7 \Big( (\theta^2)/(2) \Big) - 6\int {csc(\theta)cot(\theta)} \, d\theta`
4. [Integral] Trigonometric Integration:
   `\displaystyle \int {\big[ 7\theta - 6csc(\theta)cot(\theta) \big]} \, d\theta = 7 \Big( (\theta^2)/(2) \Big) - 6[-csc(\theta)] + C`
5. Simplify:
   `\displaystyle \int {\big[ 7\theta - 6csc(\theta)cot(\theta) \big]} \, d\theta = 6csc(\theta) + (7x^2)/(2) + C`

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration