Question

Which shows the following expression after the negative exponents have been eliminated? xy^-6/x^-4y^2, x=/ 0, y=/ 0.

A. x^4/y^2x^6y^6
B. xx^4/y^2y^6
C. x^4/y^2xy^6
D. x^4y^2/xy^6

Answer 1

it should be option b

Answer 2

Answer:- B is the right answer,we get
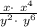`(x\cdot\ x^4)/(y^2\cdot\ y^6)` after negative exponents have been eliminated.

Explanation:-

Given expression :-
`(xy^(-6))/(x^(-4)y^2),x\\eq 0\ and\ y\\eq0`

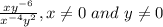
Rewriting the expression

`(xy^(-6))/(x^(-4)y^2)=(x)/(x^(-4))*(y^(-6))/(y^2)`

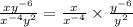
Now, to eliminate the negative exponents multiplying and dividing the expression by
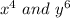`x^(4)\ and \ y^(6)` ,we get

`(x)/(x^(-4))*(x^4)/(x^4)*(y^(-6))/(y^2)*(y^6)/(y^6)=(x\cdot\ x^4)/(x^(-4)\cdot\ x^4)*(y^(-6)\cdot\ y^6)/(y^2\cdot\ y^6)`

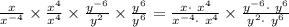
we know that
`a^n*\ a^m=a^(n+m)` [by exponents law]

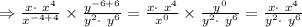`\Rightarrow(x\cdot\ x^4)/(x^(-4+4))*(y^(-6+6))/(y^2\cdot\ y^6)=(x\cdot\ x^4)/(x^(0))*(y^(0))/(y^2\cdot\ y^6)=(x\cdot\ x^4)/(y^2\cdot\ y^6)` ....> which is option B.

Therefore B is the right answer.