(a) Using Newton's Law of Cooling,
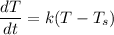
, we have
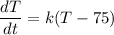
where T is temperature after T minutes.
Separate by dividing both sides by T - 75 to get
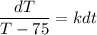
. Integrate both sides to get
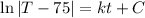
.
Since
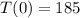
, we solve for C:
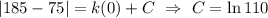
So we get
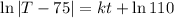
. Use T(30) = 150 to solve for k:
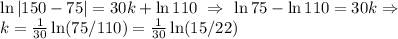
So
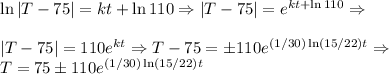
But choose Positive because T > 75. Temp of turkey can't go under.
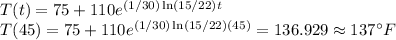
(b)
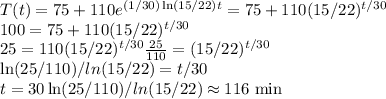
Dogs of the AMS.