Question

Solve the limit given on the picture

Answer 1

Pull out the highest power of
`n` from each radical expression, then divide through the numerator and denominator by the largest power of
`n` overall.

The largest power in the cube root is
`n^2`; the largest power in the fourth root is
`n^(12)`:


`\displaystyle\lim_(n\to\infty)((n^2-1)^(1/3)+7n^3)/((n^(12)+n+1)^(1/4)-n)=\lim_(n\to\infty)\frac{n^(2/3)\left(1-\frac1{n^2}\right)^(1/3)+7n^3}{n^3\left(1+\frac1{n^(11)}+\frac1{n^(12)}\right)^(1/4)-n}`

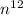
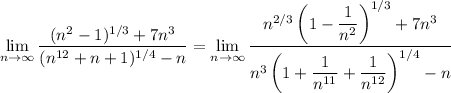
Now the largest power in the numerator and denominator is
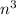
`n^3`, so we get


`=\displaystyle\lim_(n\to\infty)\frac{\frac1{n^(7/3)}\left(1-\frac1{n^2}\right)^(1/3)+7}{\left(1+\frac1{n^(11)}+\frac1{n^(12)}\right)^(1/4)+\frac1{n^2}}`

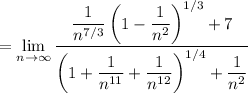
Every term containing
`n` approaches 0 as
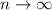
`n\to\infty`, which leaves us with


`=\displaystyle\lim_(n\to\infty)(0(1-0)^(1/3)+7)/((1+0+0)^(1/4)+0)=\frac71=7`