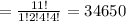Question

Find the number of distinguishable permutations of the letters m, i, s, s, i, s, s, i, p, p, i.

Answer 1

we have been asked to find the number of distinguishable permutations of the letters m, i, s, s, i, s, s, i, p, p, i.

Here we can see

m appears 1 time.

i appears 4 times.

S appears 4 times.

p appears 2 times.

Total number of letters are 11.

we will divide the permutation of total number of letters by the permutation of the number of each kind of letters.

The number of distinguishable permutations
`=(11!)/(1!2!4!4!) \\`

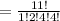
Hence the number of distinguishable permutations
`=(11!)/(1!2!4!4!)=34650 \\`