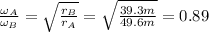Question

Two formula one racing cars are negotiating a circular turn, and they have the same centripetal acceleration. however, the path of car a has a radius of 49.6 m, while that of car b is 39.3 m. determine the ratio of the angular speed of car a to the angular speed of car

b.

Answer 1

The centripetal acceleration of a car following a circular path is:

`a_c = \omega^2 r`
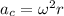
where
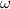
`\omega` is the angular speed of the car, and r is the radius of the orbit.

The problem says that the centripetal acceleration of car A is equal to that of car B, so we can write

`a_(cA) = a_(cB)`
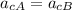
which becomes

`\omega_A^2 r_A = \omega_B ^2 r_B`
or

`(\omega_A)/(\omega_B) = \sqrt{ (r_B)/(r_A) }`

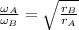
and by using the radii of the two orbits,
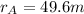
`r_A = 49.6 m` and
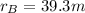
`r_B = 39.3 m`, we can find the ratio between the two angular speeds:

`(\omega_A)/(\omega_B)= \sqrt{ (r_B)/(r_A) }= \sqrt{ (39.3 m)/(49.6 m) } =0.89`