Question

Solve for x similar triangles

Answer 1

Hey there :)

We are given the information saying they are similar triangles

This means we can create a ratio of sides

Bigger Δ : Smaller Δ
Side 1 | 18 : 6
Side 2 | 24 : unknown
Side 3 | unknown : x

Sincw, we know theside 1 lengths of both triangles, we can find the ratio


`(18)/(6)` = 3
So, the bigger triangle is 3 times larger than the smaller triangle

Before, we work with x, notice that we are not given the length of the corresponding side of x in the bigger triangle. Which means, since we know the scale factor ( × 3 ), we can find side 2 to find the length of the corresponding unknown of the smaller triangle

24 : unknown = 3 →
`(24)/(unknown) = 3`
Make "unknown" the subject


`(24)/(3) = unknown`
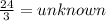
unknown length of small triangle = 8

We know the base length of the small Δ to be 6, the longer side to be 8, we still need to find x.

Since x is the hypotenuse, we can use Pythagoras theorem:
( side 1 )² + ( side 2 )² = ( hypotenuse )²
( 6 )² + ( 8 )² = ( x )²
36 + 64 = x²
100 = x²
√100 = √x²
x = 10

Answer 2

We first need to find how many times smaller the small one is.
To do that, divide 18 by 6, because those are the 2 numbers that we know, the numbers that we can compare. The answer will be 3, so the big one is 3 times more than the smaller one, which tells us that we need to divide 3 from the bigger triangle to find the lengths for the smaller one. 24 divided by 3 equals to 8. So x equals to 8