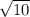Question

Q4.) Solve the equation by the method of your choice.

Answer 1

Hey there!

First, you must find the common denominator of the equation.

To find the common denominator, first take a look at all the factors of each denominator:

x: x
x+4: x+4
6: 2*3

Next, because you do not have a common multiple in the denominators, you would multiply the denominators together to create one common multiple:
6(x)(x+4). This would be used to remove the fractions from the equation to make it easier to solve.

Now, multiply the common multiple 6(x)(x+4) to the entire equation:
(6(x)(x+4)) × (
`(1)/(x)` +
`(1)/(x+4)` =
`(1)/(6)`)

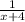
When you multiply the factor to the equation, the x in the common factor would cancel out the x in
`(1)/(x)` resulting in just 6(x+4).

The x+4 would cancel out the x+4 factor in
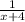
`(1)/(x+4)` resulting in just 6x.

The 6 would cancel out the 6 in
`(1)/(6)` resulting in just x(x+4).

As a result, when you multiply the common factor 6(x)(x+4) to
`(1)/(x)` +
`(1)/(x+4)` =
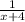
`(1)/(6)`, you will get
(6(x+4))+ 6x = x(x+4)

Now, simplify the equation further:
(6(x+4))+ 6x = x(x+4)
6x+24+6x=x^2+4x (I have distributed the values in the parentheses)
12x+24=x^2 + 4x (I combined like terms on both sides)
0=x^2-8x-24 (I have moved all terms to one side so that the x values can be solved for using the quadratic formula)

Because this quadratic does not factor evenly, we must use the quadratic formula in order to find the exact x values:
x=
`(-b±√(b^2-4ac) )/(2a)`

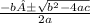
Your a value is 1, your b value is -8, and your c value is -24:
x=
`(-(-8) ±√((-8)^2-4(1)(-24)) )/(2(1))`
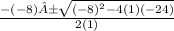
x=
`(8 ±√(64+96) )/(2)`
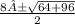
x=
`(8 ±√(160) )/(2)`
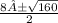
x=
`(8 ±4√(10) )/(2)`
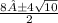
x=4±2
`√(10)`

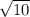
Therefore, your x values are 4+2
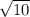
`√(10)` and 4-2
`√(10)`